Contents
Merkle Trees and Merkle Roots Help Make Blockchains Possible
Merkle trees and Merkle roots are a key part of the blockchain cryptography underpinning Bitcoin and other blockchain networks.
Updated October 21, 2021 • 4 min read
Summary
A Merkle tree is a data structure that can help prove the integrity of a dataset while significantly reducing the memory requirements needed to do so. This utility is achieved via one-way hash functions that merge layers of data into a singular Merkle root capable of validating all the data contained in the associated Merkle tree. The Merkle tree data architecture is a key component of public blockchains, and is used in peer-to-peer (P2P) networks such as file-sharing applications, Bitcoin, and other decentralized blockchains.
Merkle Trees: “Let’s Hash It Out”
Named after Stanford professor Ralph Merkle, Merkle trees and Merkle roots were proposed as a new data-verification process in his 1979 paper, “A Certified Digital Signature.” Using one-way functions called hash functions, a Merkle tree — also called a binary hash tree — takes data and hashes it together to create a Merkle root that can serve as a way to verify data in a Merkle tree while using significantly less memory than previous methods. In the Bitcoin network, a Merkle root is created by hashing all the transaction hashes together in pairs — producing a unique hash for all the transactions in a block.
Thirty years after the publication of “A Certified Digital Signature,” Satoshi Nakamoto wrote about Merkle trees and even included one of Ralph Merkle’s papers in the references for the Bitcoin whitepaper. Without Merkle trees and their associated Merkle roots, the trustless value transfer of blockchains likely wouldn’t have been possible.
Merkle Trees and Blockchain
Computer science uses the term “tree” to describe anything with a branching data structure. Unlike the CO2-consuming kind, Merkle trees have their leaves at the bottom and a singular root at the top. When it comes to blockchains, a Merkle tree has three key components:
Leaf Nodes
Non-Leaf Nodes
Merkle Root
At the bottom of the Merkle tree, you have leaf nodes. These are the transaction hashes — more commonly known as transaction IDs (TXIDs) — of every crypto transaction in a block. If you look up a transaction on a block explorer, you’re looking at the transaction hash.
These leaf nodes are then hashed together in pairs to create a layer of non-leaf nodes above the leaf nodes. They are called non-leaf because unlike leaf nodes, they don’t contain transaction IDs (or hashes), and instead simply store the hash of the two leaf nodes below it that it represents. As a result, the non-leaf node layer above the leaf nodes will have half as many hashes — or nodes — as the leaf node layer.
These non-leaf node layers continue to be hashed together in pairs, creating half as many nodes per layer as the tree narrows on its way up. The last non-leaf node layer will contain two nodes. This is where the final hashing in a Merkle tree takes place and it creates the Merkle root.
The Merkle root, through the hashing process, can now be used to verify the leaf nodes (transaction IDs/hashes) at the bottom of the Merkle tree. If you’re familiar with how Bitcoin works, you might know that transaction hashes are turned into a single hash that is included in the block header. This single hash is the Merkle root, which is sometimes called the root hash.
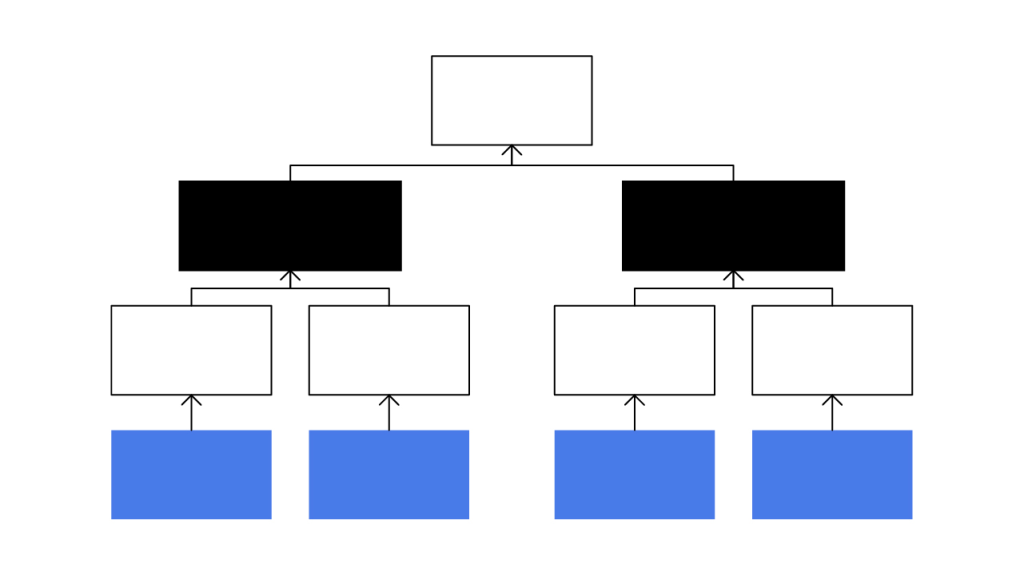
Bitcoin Merkle Tree Example
While a block can contain hundreds or thousands of crypto transactions, let’s look at an example with eight transactions:
The eight transaction hashes — more commonly known as transaction IDs — constitute the leaf-node level at the bottom of the tree. These transactions are hashed together in pairs.
The paired hashes create four non-leaf nodes, which don’t contain transaction hashes. These non-leaf nodes are then hashed together in pairs.
This creates another two non-leaf nodes in the Merkle tree. These are then hashed together in a final pairing.
This creates the singular Merkle root at the top of the Merkle tree. The Merkle root contains a single hash that can validate every single transaction hash in the block. As such, a Merkle root is included in the block header of every block on the blockchain.
Merkle trees are a binary data structure that require an even number of leaf nodes or transaction hashes. If a block were to have an uneven number of transaction hashes, the last transaction hash would be doubled and hashed with itself. For instance, if the above example had seven transactions, the seventh transaction would be duplicated and hashed with its copy. The remainder of the tree would then proceed in the same manner as the eight-transaction example above.
Merkle Roots in Blockchain: Why?
In theory, instead of using a Merkle tree, you could just hash all the TXIDs together in one batch. However, if you did this and wanted to check a specific transaction, you’d need to know every TXID in the associated block. This would require a lot of memory to be stored and transmitted across the network. With a Merkle tree, you can check a TXID using the Merkle root — without needing to know every single TXID in a block. In essence, a Merkle tree is a great way to prove that something is in a dataset without needing to download the full set. This is why Merkle trees are considered more efficient at storing and verifying transaction data than simple hashing.
Below are some of the major benefits of using Merkle trees for blockchains:
They significantly reduce the memory needed to verify that data has maintained its integrity and hasn’t been altered.
They require less data to be broadcast across the blockchain network to verify data and transactions. This improves the efficiency of a blockchain.
They allow for Simple Payment Verification (SPV), which helps you to verify a transaction without downloading an entire block or blockchain. This allows you to send and receive transactions using a light-client node — more commonly known as a crypto wallet.
Whereas full nodes secure the network and store an entire history of the blockchain, these light nodes can use the Merkle root in the block header of a block to verify a transaction. As Bitcoin has hundreds of thousands of blocks containing thousands of transactions each, these light nodes or crypto wallets wouldn’t be able to function efficiently without the blockchain implementing the Merkle tree and Merkle root data architecture.
To put this into clearer context, as of April 2021 the Bitcoin blockchain contained about 330 gigabytes of data. Further, while the Merkle root included in a block header is just 80 bytes, a full Bitcoin block is more than 1,000 times larger. On top of all these considerations, a Bitcoin Cash (BCH) block is 8 MB (more than 100,000 times bigger than its associated block header of 80 bytes). Without Merkle trees, every single node of the network would need to keep a complete copy of every transaction that has ever occurred on a blockchain — a daunting and memory-intensive task. Can you imagine if you had to store 330 GB of data on your phone just to send and receive bitcoin using a mobile wallet?
Merkle Trees in Bitcoin and Beyond
The efficiencies in data storage, transfer, and verification gained from Merkle trees were a key technical component of Bitcoin that made its cryptographic breakthroughs possible. The Merkle tree data-storage structure used on Bitcoin is also used by Ethereum, Bitcoin’s forks (BCH for example), and many other public blockchain networks. By making SPV possible, Merkle roots derived from Merkle trees enable people around the world to send, receive, and verify transactions with crypto wallets that can be run easily and simply on a personal computer or smartphone. Merkle trees help blockchain networks efficiently and securely verify large data structures by getting down to the Merkle root of the problem.
Cryptopedia does not guarantee the reliability of the Site content and shall not be held liable for any errors, omissions, or inaccuracies. The opinions and views expressed in any Cryptopedia article are solely those of the author(s) and do not reflect the opinions of Gemini or its management. The information provided on the Site is for informational purposes only, and it does not constitute an endorsement of any of the products and services discussed or investment, financial, or trading advice. A qualified professional should be consulted prior to making financial decisions. Please visit our Cryptopedia Site Policy to learn more.

Is this article helpful?